[인공지능 개론 수업 2] 기계 학습(ML)의 주요 모델 - 2

• 차원

- 차원의 저주

1. 데이터의 차원이 커질 수록 필요한 데이터 수가 그만큼 증가하게 되고 이에 따라 모델의 성능이 저하되는 현상을 말함

2. 또한 동시에 데이터 간의 거리가 벌어져 밀도가 희소해지는데(sparse),이런 경우 거리에 기반한 알고리즘 성능이 매우 떨어짐

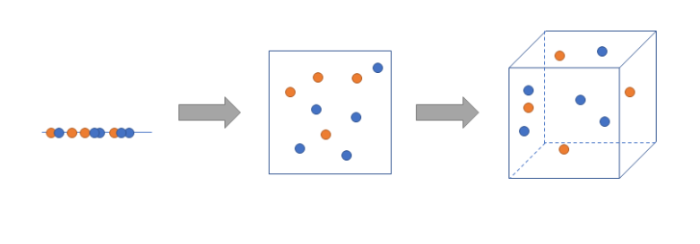
- 차원이 늘어나면 늘어날 수록 개별 데이터간 거리는 점점 멀어짐

- 피쳐가 많을 수록 피쳐가 다른 피쳐에 의해 설명 가능하게 되는 다중 공선성(Multicollinearity) 문제가 발생하게 될 가능성이 커지게됨

- 이때 차원축소를 하게되며 크게 2가지로 나뉨

1. 피쳐 선택(Feature Selection)

- 어떤 데이터의 피쳐가 a,b,c,d,e,f,g 로 있을 때, 이 중 필요한 피쳐가 a,b 만 있으면 된다고 판단하면 그냥 a,b만 가져다가 쓰는 것

2. 피쳐 추출(Feature Extraction)

- 기존의 피쳐를 살짝 변형하면서 압축합니다. 피쳐 선택이 그냥 있는 것 "그대로" 골라오는 것이었다면, 피쳐 추출은 있는 것을 살짝 변형시키면서 압축을 시킴

 

PCA(Principal Component Analysis)

"가장 큰 분산을 가지는 축을 기반으로 차원을 축소시키는 기법"

 

LDA(Linear Discriminant Analysis)

LDA또한 PCA와 마찬가지로 차원 축소를 하는 방법 중 하나

다만, PCA와의 차이라고 한다면 클래스 분류까지 용이하게 해준다는 것

PCA는 데이터의 클래스들이 어떻게 분포했는지는 상관하지 않고, 데이터들의 분포만 보고 축을 형성했음

그러나 LDA는 분포 보단 클래스를 나누는 것에 좀 더 초점을 맞췄다고 할 수 있음

 

• Regression
  • Linear Regression
    • Y = A*X + B
  • Polynomial Regression
    • Y = A*X2 + B*X + C
  • Multiple / Multinomial Regression
    • Z = A*X2 + B*X*Y + C*Y2 + D
    •  multinomial regression when the outcome variable is categorical (with more than two categories

 

• Logistic Regression(이진 분류 & 다중 분류)
  • 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1사이 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘임
• 로지스틱 회귀와 시그모이드 함수
  • 로지스틱 회귀는 여러 특성을 고려했을 때 특정값 A로 분류될 확률 구하는 알고리즘임
  • 이때 여러 특성이 고려된 관계식은 서두에서 말한 거와 같이 로지스틱 회귀는 선형방정식을 사용함
  • x = a+ a'(특성 1) + b(특성2)
  • 식이 위와 같다면 선형방정식의 X값은 실수가 됨
  • 그런데 우리는 A로 분류될 확률을 구해야 하기 때문에 X값이 0~1가 되도록하여야 하며 '시그모이드 함수'를 통해 변형함
  • 시그모이드 함수의 식과 그래프는 다음과 같음

• 다중분류 로지스틱 회귀 분석
  • 구분해야할 클래스가 3개 이상일 때 우리는 다중 분류 로지스틱 회귀분석을 이용할 수 있음
  • 이진 분류 때와 다른 점은 확률로 변환시켜주는 함수를 시그모이드 함수가 아니라 소프트맥스 함수를 사용한다는 것임
  • 다중 분류 로지스틱 회귀분석은 각 클래스마다 Z값을 계산함
  • 이진 분류였을 때는 양성 클래스의 Z값만 계싼했음, 왜냐하면 양성클래스만 계산해도 나머지 하나의 확률을 유추할 수 있기 때문
  • 하짐나 다중 분류의 경우 1개의 클래스의 여집합이 2개 이상이 되기 때문에 하나의 Z값만으로는 다른 클래스의 확률을 유추할 수 없게 됨
  • 그래서 다중 분류 로지스틱 회귀함수는 각 클래스(분류값)마다 Z값을 구하는 것이고 이를 확률로 변환시키기 위해 소프트맥스 함수를 이용함
• 소프트맥스 함수(Softmax Function)
  • 소프트맥스 함수는 여러 개의 선형 방정식의 출력값을 0~1 사이로 압축하고 모든 클래스의 확률을 더했을 때 1이 되도록 만들어주는 함수임
  • 수학적인 식은 아래와 같음
  • 각 클래스의 z값을 지수로 하는 자연상수 e를 모두 더한 값을 분모로 하고, 각각 z값을 지수로 하는 자연상수 e를 분모로 나누면 해당 z값을 확률로 변환해주는 역할을 소프트맥스 함수가 대신한 것

- 참조 코드 : 로지스틱 회귀

https://blog.naver.com/psycomaniac/222461673102

로지스틱 회귀(feat. 시그모이드 함수)

 

- 참조코드 : 다중회귀/소프트맥스

https://blog.naver.com/PostView.naver?blogId=psycomaniac&logNo=222472359036 

다중 분류 로지스틱 회귀분석(feat.소프트맥스)