Optimization : Lagrange Dual Problem & Strong duality and Karush-Kuhn-Tucker Conditions
- 통계학 또는 머신러닝에서, 모형의 학습은 목적함수를 최소화(혹은 최대화)하여 모형의 parameter의 최적 값을 찾음으로써 이루어짐
- Lagrangian metod는 제약 하 최적화 문제를 해결하는 가장 대표적인 방법 중 하나
- Karush-Kuhn-Tucker조건 : strong duality가 보장이 되었을 때, Karush-Kuhn-Tucker조건은 어떤 벡터들이 최적화 문제의 primal solution과 dualsolution이 되는 것과 필요 충분 관계의 조건이 된다는 점에서 매우 의미가 있는 조건
* Optimization
- 어떤 함수의 optimum point, 즉 그것이 최소이거나 혹은 최대인 지점을 찾는 과정을 optimization
- 대부분 Optimization은 아래와 같은 식으로 표현할 수 있음

- 간단히 생각해보면 위에서 f(x)는 loss function이고, g(x)는 일종의 constriants로 생각하면 됨
- 하지만, 항상 이런 function들의 optimum point를 찾을 수 있는 것은 아님
- 간단하게 생각했을 때 이런 point를 찾는 방법은 미분을 하고 그 값이 0이되는 지점을 찾는 것인데, 미분 자체가 되지 않는 함수가 존재할 수 있으며, 미분값이 0이라고 해서 반드시 극점인 것은 아니기 때문
- 따라서 대부분의 경우에 이런 방법으로 극점을 구하는 것음 불가능, 매우매우 특수한 일부 경우에 대해 완전한 optimum을 찾기 위한 방법으로 convex optimization 이 있음
A. Convex Optimization
- Convex function은 convex한 function(볼록함수)을 의미
- 먼저 convex set이란 어떤 set이 convex하다는 의미는 그 set에 존재하는 어떤 점을 잡아도 그 점들 사이에 있는 모든 점들 역시 그 set에 포함되는 set을 convex set이라고 부름
- 따라서 convex한 set을 그림으로 그리게 되면 움푹하게 파인 지점 없이 약간 동글동글한 모양을 지니고 있음
- Convex function은 domain이 convex set이며, 함수는 다음과 같은 성질을 만족해야함


- 하지만 위 함수와 달리 아래함수는 optimal point가 한개가 아님

- unique한 optimal point를 찾기 위해서는 하나의 조건이 더 필요함
- strictly convex라는 조건 -> 위의 식에서 = 이 빠진 형태로, ≤ 가 < 으로 바뀌는 것
- 이렇게 되면 strictly convex function은 minimum point가 unique하게 존재하기 때문에, 이런 convex function에 대해서 우리는 어떤 optimization algorithm을 design할 수 있음
A-1. Convex Optimization에서 사용할 수 있는 알고리즘
http://sanghyukchun.github.io/63/
1. Gradient Descent Method- 미분 가능한 convex function의 optimum point를 찾는 가장 popular한 방법 중 하나- 장점이라면 많은 application에 implement하기 매우 간단하고, 모든 차원과 공간으로 확장할 수 있으며, 수렴성이 항상 보장된다는 것이지만, 속도가 느리다는 단점이 존재
- 쉽게 예시를 들자면 산 정상에서 가장 빨리 지면으로 내려가야됨 -> 주변에 기울기 가파른 지점 찾아서 내려가고 또 내려가고 반복해서 언젠가는 기울기가 0이라는 지점에 도달

- x(k) 는 k번 째 iteration에서의 x의 값이며 ∇f(x(k)) 는 그 지점에서의 gradient 값
1. set iteration counter k=0, and make an initail guess x0 for the minimum
2. Compute −∇f(x(k))
3. Choose η(k)η(k) by using some algorithm
4. Update x(k+1)=x(k)−η(k)∇f(x(k)))x(k+1)=x(k)−η(k)∇f(x(k))) and k = k+1
5.Go to 2 until ∇f(x(k)))<ϵ
- 만약 function이 convex하다면, 이런 방법으로 x를 계속 update하다보면 적절한 ηη를 취했을 때 이 algorithm은 global unique optimum으로 수렴하게 됨
- 이때 η를 Step size라고 일컫는데, 이 step size를 어떻게 설정하느냐에 따라 performance가 좌우된다
- 만약 stepsize를 너무 작게하면iteration을 너무 많이 돌아서 전체 performance자체가 저하될것
- 그렇다고 너무 크게하면minima에 converge를 하는것이 아니라 그 주변에서diverge를 할수도 있음

2. Newton method
3. lagrange multiplier
* Strong duality
- Strong duality는 primal problem과 dualproblem을 기반으로 하기 때문에, 먼저 이 둘이 뭔지 알아야함
- 이에 앞서 convex optimization의 standard form을 생각해보자

- 와 들은 모두 convex function 이고, equality constraint에서 임
- 우리는 그중 p < d인 경우에 관심이 있고, rank(A) = p 라고 가정하자 (더 정확히, 우리는 항상 A의 rank가 p인 full-rank 행렬을 만들 수 있으니 그렇다고 가정할 수 있음)
* full-rank : 역행렬을 가질 수 있는 정방행렬
- Primal probelm을 알기 위해서는 두가지 function(Lagrange function, dual function) 알아야함
- Primal problem:
A problem that we start with - Dual problem:
Another problem which is closely related to the primal problem
1. Lagrange function
- Lagrange function은 와 같이 표현
- 식은 총 세 가지 arguments로 표현
- 는 interested optimization variable이고
- 는 size ,
- 는 size 의 real-valued vector
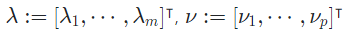
- 참고로 와 의 size는 각각 inequality, equality constraint의 개수와 같음
- 이들을 종합한 Lagrange function의 꼴은 다음과 같음
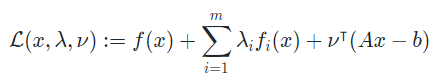
- 각 ( 번째) constraint에 곱해져 있는 상수 와 를 Lagrange multiplier 라고함
2. Dual function
- Dual function

- x가 entire space 에 속해 있음- Entire space는 곧(x가 존재할 수 있는) valid space임- 이는 정의역(혹은 domain)과 같고, problem에서의 optimization variable x를 생각해보면- 으로 정의할 수있음
- ㅇㅇㅇ