부스팅 앙상블 (Boosting Ensemble) 2-1: Gradient Boosting for Regression

전체적인 내용은 StatQuest라는 유투버의 Gradient Boost Part 1: Regression Main Ideas과 Gradient Boost Part 2: Regression Details를 참고했습니다. Gradient Boosting에 대해 가장 정리가 잘 된 설명자료입니다 (영어이지만 시각자료도 많고, 화면에 자막도 있어서 알아듣기 쉽습니다)

 

AdaBoost VS Gradient Boosting

AdaBoost와 Gradient Boosting 두 모델의 공통점은 부스팅 앙상블 기반의 알고리즘이라는 것입니다. 부스팅 앙상블의 대표적인 특징은 모델 학습이 sequential합니다. 즉, 먼저 생성된 모델의 예측값이 다음 모델 생성에 영향을 줍니다.
하지만 이 외에 두 모델은 상당한 차이점이 있습니다.

 

AdaBoost에 비교되는 Gradient Boosting의 대표적인 차이점은 세 가지 정도로 정리할 수 있습니다.

1. Weak learner: Stumps VS A leaf & Restricted trees
2. Predicted value: Output VS Pseudo-residual
3. Model weight: Different model weights (amount of say) VS Equal model weight (learning rate)

---

1. Weak learner

앙상블 모델의 기본이 되는 weak lerner가 다름

-AdaBoost에서는 weak learner로 stump (한 개 노드와 두 개의 가지를 갖는 매우 작은 decision tree) 를 사용

- Gradient Boosting에서는 restricted tree를 사용(restricted tree란, maximum number of leaves로 성장에 제한을 둔 decision tree)

-  Gradient Boosting의 첫 번째 weak learner는 모든 샘플의 output 평균을 값으로 갖는 하나의 leaf

 

2. Predicted value

각 모델이 예측하는 정보가 다름

[AdaBoost]

- 각 stump들은 모두 실제 output 값을 예측하는 모델

- 따라서 이 값을 평균내거나 가중치를 곱한 평균을 통해, 실제 값에 가까운 예측값을 만들어냄

 

[Gradient Boosting]

- Gradient Boosting에서 각 restricted tree들이 예측하는 값은 실제 output과 이전 모델의 예측치 사이의 오차 (pseudo-residual)

- 최종 예측 시에는 각 모델의 오차를 scaling 후, 합하는 과정을 통해 실제 값에 가까운 예측값을 만들어냄

Pseudo-residual에서 
Pseudo
라는 단어가 붙은 이유는 linear regression 에서의 residaul과 구별하기 위해서입니다.
Gradient Boosting에서 어떤 Loss function을 사용하느냐에 따라 residual과 동일할 수도, 비슷할 수도 있기에 이런 이름을 붙였다고 함

3. Model weight

각 모델에 대해 가중치를 주는 방식이 다름

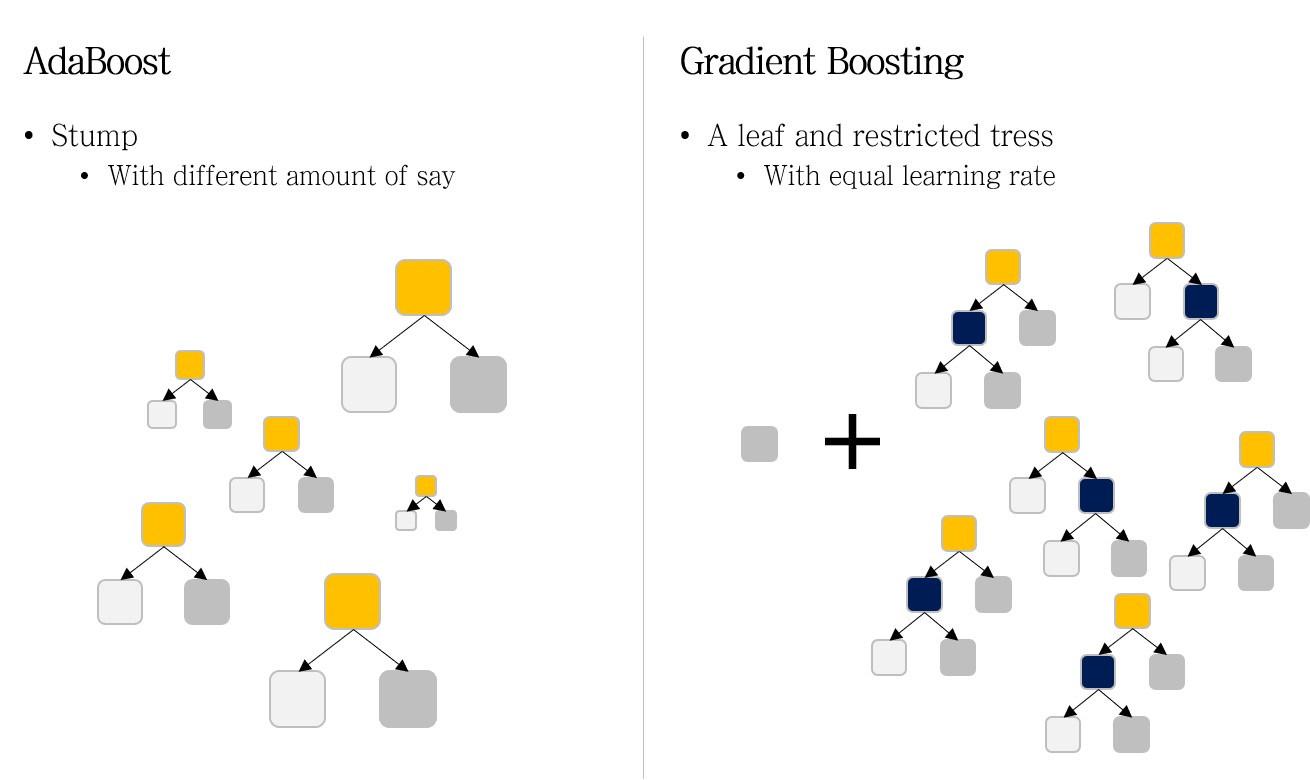
- 위 그림에서 알 수 있듯이 AdaBoost에서는 각 모델의 크기가 다른 반면, Gradient Boosting에서는 크기가 동일한 것을 알 수 있음

- AdaBoosting에서는 amoung of say αtαt를 인풋 xx에 대한 각 모델의 예측값 ht(x)ht(x)에 곱하여 최종 예측값을 계산

 

Gradiend Boosting for Regression

Gradient Boosting은 회귀 (Regression)와 분류 (Classification) 문제에 모두 사용 모두 가능

두 알고리즘은 전체적으로는 비슷하지만, 디테일 면에서 다름

알고리즘의 공통점을 요약하면 아래와 같습니다.

Create decision trees to predict residual (observed value – predicted value) of **__**, with limitation of maximum number of leaves.

두 알고리즘은 진한 부분의 블랭크 (_)에 무엇이 들어가느냐가 다릅니다.

본 포스팅에서는 상대적으로 쉬운 Gradient Boosting for Regression 알고리즘을 먼저 정리해보도록함

 

1. Create a first leaf
2. Calculate pseudo-residuals
3. Create a next tree to predict pseudo-residuals
4. Repeat 2-3

• (Test) Scale and add up the results of each tree

1. Create a first leaf

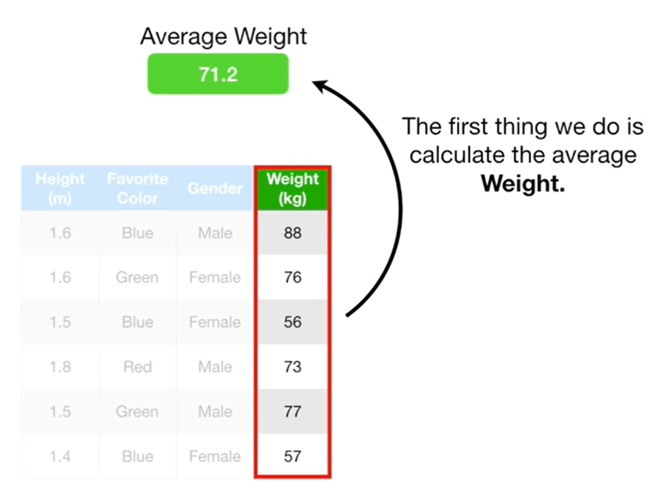
- First model로 leaf를 만듦

- 이 Leaf가 갖는 값 F0(x)은 training data의 모든 output의 평균

- 초기값으로 output의 평균값을 사용하는 이유는 아래 수식을 미분해서 풀면 됨

2. Calculate pseudo-residuals

Pseudo-residual (실제값 - 예측값)을 계산합니다.

Compute \(r{im}=-\frac{\partial L(y_i, F(X_i))}{\partial F(X_i)}\), where \(F(x)=F{m-1}(x)\) for i=1,…,n

3. Create a next tree to predict pseudo-residual

3-1. Create a tree

주어진 데이터 (Height, Favorite color, Gender)를 바탕으로 Pseudo-residual을 예측하는 decision tree를 만듭니다. 아래와 같은 tree가 만들어짐

3-2. Calculate representative value by leaves

Terminal node (leaf)마다 예측결과를 평균내줌

결과적으로 수많은 데이터 값이, decision tree의 최종 leaf에 따라 몇 종류의 예측값으로 축약됨

 

4. Repeat 2-3

다시 각 샘플에 대해 pesudo-residual을 계산하고, 이를 바탕으로 decision tree를 만드는 과정을 반복합니다.

이 때 주목할 점으로, 첫 번째 모델의 pseudo-residual보다 두 번째 모델의 pseudo-residual이 감소한 것을 확인할 수 있습니다 

(Test) Scale and add up the results of each tree.

입력값 x에 대한 각 모델의 residual 예측값 ht(x)에 동일한 Learning rate η (ν)를 가중치로 곱한 뒤 합계를 구합니다.

Update \(Fm (x)=F{m-1} (x) + \nu \sum{j=1}^{J_m} \gamma{jm} I(x \in R_{jm})\)

ν는 η 대신 쓰인 learning rate 입니다.

Output: F(x)F(x)