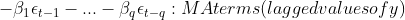1. ARIMA모델

ARIMA(Autoregressive Integrated Moving Average)

ARIMA는 Autoregressive Integrated Moving Average의 약자로, Autoregressive는 자기회귀모형을 의미하고, Moving Average는 이동평균모형을 의미한다.

즉, ARIMA는 자기회귀와 이동평균을 둘 다 고려하는 모형인데, ARMA와 ARIMA의 차이점은 ARIMA의 경우 시계열의 비정상성(Non-stationary)을 설명하기 위해 관측치간의 차분(Diffrance)을 사용한다는 차이점이 있다.
ARMA와 ARIMA 외에도 ARIMAX 등의 방법도 있는데, 이는 본 포스트에서 살펴보지 않는다.

• AR: 자기회귀(Autoregression). 이전 관측값의 오차항이 이후 관측값에 영향을 주는 모형이다. 아래 식은 제일 기본적인 AR(1) 식으로, theta는 자기상관계수, epsilon은 white noise이다. Time lag은 1이 될수도 있고 그 이상이 될 수도 있다.
  

  

• I: Intgrated. 누적을 의미하는 것으로, 차분을 이용하는 시계열모형들에 붙이는 표현이라고 생각하면 편하다.
• MA: 이동평균(Moving Average). 관측값이 이전의 연속적인 오차항의 영향을 받는다는 모형이다. 아래 식은 가장 기본적인 MA(1) 모형을 나타낸 식으로, beta는 이동평균계수, epsilon은 t시점의 오차항이다.
  

  

현실에 존재하는 시계열자료는 불안정(Non-stationary)한 경우가 많다. 그런데 AR(p), MA(q) 모형이나, 이 둘을 합한 ARMA(p, q)모형으로는 이러한 불안정성을 설명할 수가 없다.
따라서 모형 그 자체에 이러한 비정상성을 제거하는 과정을 포함한것이 ARIMA모형이며 ARIMA(p, d, q)로 표현한다.

• 

• 

• 

• 

• 

• 

위와 같은 특징에 따라 ARMIA(p, d, q)는 AR, MA, ARMA를 모두 표현할 수 있다.

• AR(p) = ARIMA(p, 0, 0)
• MA(q) = ARIMA(0, 0, q)
• ARMA(p, q) = ARIMA(p, 0, q)

이 외에도 ARIMA와 관련한 많은 내용이 있으나, 본 포스트에서는 생략하고 이후 포스트 진행에 필요한 부분들이 있으면 간략하게 설명하겠다. 참고할만한 서적으로는 ARIMA를 포함하여 통계적 시계열분석의 Standard라고 할 수 있는 Box, George; Jenkins, Gwilym (1970). Time Series Analysis: Forecasting and Control.(아마존 링크)를 참조하시면 좋을 듯 하다.

1.정상성

-정상성(stationarity)을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관

-추세나 계절성이 있는 시계열은 정상성을 나타내는 시계열이 아니다

-백색잡음(white noise) 시계열은 정상성을 나타내는 시계열 / 언제 관찰하는지에 상관이 없고, 시간에 따라 어떤 시점에서 보더라도 똑같이 보일 것이기 때문

-일반적으로는, 정상성을 나타내는 시계열은 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않을 것입니다. (어떤 주기적인 행동이 있을 수 있더라도) 시간 그래프는 시계열이 일정한 분산을 갖고 대략적으로 평평하게 될 것을 나타낼 것입니다.

Figure 8.1: 다음의 시계열 중에서 어떤 것이 정상성을 나타낼까요? (a) 200 거래일 동안의 구글 주식 가격; (b) 200 거래일 동안의 구글 주식 가격의 일일 변동; (c) 미국의 연간 파업 수; (d) 미국에서 판매되는 새로운 단독 주택의 월별 판매액; (e) 미국에서 계란 12개의 연간 가격 (고정 달러); (f) 호주 빅토리아 주에서 매월 도살한 돼지의 전체 수; (g) 캐나다 북서부의 맥킨지 강 지역에서 연간 포획된 스라소니의 전체 수; (h) 호주 월별 맥주 생산량; (i) 호주 월별 전기 생산량.

 

그림 8.1에 나타낸 9개의 시계열을 살펴봅시다. 이 중에서 어떤 것이 정상성을 나타내는 시계열이라고 생각합니까?

분명하게 계절성이 보이는 (d), (h), (i)는 후보가 되지 못합니다. 추세가 있고 수준이 변하는 (a), (c), (e), (f), (i)도 후보가 되지 못합니다. 분산이 증가하는 (i)도 후보가 되지 못합니다. 그러면 (b)와 (g)만 정상성을 나타내는 시계열 후보로 남았습니다.

언뜻 보면 시계열 (g)에서 나타나는 뚜렷한 주기(cycle) 때문에 정상성을 나타내는 시계열이 아닌 것처럼 보일 수 있습니다. 하지만 이러한 주기는 불규칙적(aperiodic)입니다 — 먹이를 구하기 힘들만큼 살쾡이 개체수가 너무 많이 늘어나 번식을 멈춰서, 개체수가 작은 숫자로 줄어들고, 그 다음 먹이를 구할 수 있게 되어 개체수가 다시 늘어나는 식이기 때문입니다. 장기적으로 볼 때, 이러한 주기의 시작이나 끝은 예측할 수 없습니다. 따라서 이 시계열은 정상성을 나타내는 시계열입니다.

 

2.차분

-정상성을 나타내지 않는 시계열을 정상성을 나타내도록 만드는 한 가지 방법을 나타냅니다 — 연이은 관측값들의 차이를 계산하는 것입니다. 이것은 차분(differencing)로 알려져 있습니다.