2022. 8. 17. 16:44ㆍAI study
- 비선형 최소자승 Nonlinear Least Square 문제를 푸는 대표 방법
- Gauss-Newton method와 Gradient Descent 방법이 결합된 방법론
- 1944년 Levenberg Algorith이 1963년 Marquardt가 보완한 방법론으로 보통 generic curve fitting prblem을 풀기위해 사용되지만 local minimum을 주로 찾게되는 단점이 있음
- 수식적으론 다음과 같다

- 이 방법론을 사용하면 기존의 Hessian matrix로 표현하는 것을 Jacobian Matrix로 정의가 가능해지고 이를 통해 위와 같은 수식을 볼 수 있음
- 위 방법을 사용해 singular문제를 회피하면서도 효과적으로 해를 찾을 수 있음
- 다른 말로 Damped Least Squares(DLS)라고도 일컫어짐
- 그러나 Inverse Matrix를 구해야하기 때문에 시간 복잡도적 측면에서 오래 걸림
1. 최소자승법 & 가중최소자승법
2. Gradient Descent 탐색 방법
3. 뉴턴법 (뉴턴-랩슨법)
4. 가우스-뉴턴법
5. Levenberg-Marquardt 방법
6. 마무리하며
1. 최소자승법 & 가중최소자승법
- 최소자승법 : 관측값을(xi, yi), i = 1,....,n, 모델 파라미터를 p = (p1,p2,...,pm), 모델을 y = F(x,p) ,
관측값과 모델과의 오차(residual)를 ri라 할때, 오차 제곱합이 최소화 되도록 모델 파라미터 p를 정하는 방법을 최소자승법(least square method)라 함
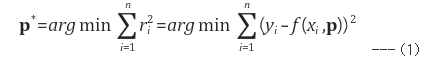
- 가중최소자승법 : 관측값의 신뢰도(중요도)가 서로 다를 경우에는 각각의 오차 제곱에 가중치 wi를 곱해서 최소화시키는 방법 (통계 쪽에서는 보통 wi = 1/σi2로 잡음. 단, σi2은 yi의 분산).

이 때 식(1), (2)의 에러합 부분을 행령 형태로 표현하면 다음과 같음

단, r = [r1, ..., rn]T, W는 wi를 대각원소로 갖는 대각행렬 (W = diag(w1, ..., wn)).
- 최소자승법은 결국 식 (3) 또는 식 (4)에 의해 주어지는 에러 함수를 최소화시키는 p를 구하는 문제로 볼 수 있으며 이는 p에 대한 미분이 E'(p) = 0, Ew'(p) = 0인 p를 구함으로써 얻어짐
- 선형(linear) 최소자승문제의 경우에는 벡터미분을 이용하여 이러한 해를 직접적으로 구할 수 있다 (closed-form solution이 존재).
☞ 최소자승 문제에 있어서 모델 f(x,p)가 모델 파라미터에 대해 선형인 경우 선형 최소자승 문제(linear least squares problem)라 부르고 그렇지 않은 경우 비선형 최소자승문제(non-linear least squares problem)라 부름
**예를들어 f(x,p) = p1*sinx + p2*cosx 라면 f(x,p)자체는 비선형 함수이지만 파라미터 p=(p1,p2)에 대해서는 선형이므로 f(x,p)에 대한 최소자승 문제는 선형(linear)문제가 됨
- f(x,p)가 p에 대해 선형인 경우에는 f(x,p)를 아래와 같이 p에 대한 일차 결합 형태로 표현할 수 있음

- 따라서, 선형 최소자승문제와 선형 가중최소자승문제의 해는 다음과 같이 closed-form 형태로 구해짐

[음함수 최소자승법]
- 만약 모델이 양함수(explicit function) 형태가 아니라 f(x,p) = 0와 같은 음함수(implicit function)형태인 경우
- 이 경우 ri = f(xi,p)이며, f(x,p)가 p에 대해 선형이면 최소자승문제를 ∑ri2 = ∥Ap∥2와 같이 표현할 수 있음
- ∑ ri2 = ∥Ap∥2를 최소화시키는 p는 A의 SVD(singular value decomposition)을 A = U∑VT라 할 때 최소 특이값(singular value)에 대응하는 V의 열벡터가 됨
※ 선형(linear) 최소자승 문제의 경우에는 pseudo inverse나 SVD(singular value decomposition)을 이용하면 해를 손쉽게 구할 수 있음
- > 비선형(non-linear) 최소자승 문제의 경우에는 closed-form solution이 없기 때문에 점진적으로 해를 찾는 방법(iterative minimization)을 사용해야함(즉, 어떤 초기값 p0에서 시작해서 점차적으로 E(p)를 최소화시키는 방향으로 p를 갱신하는 방법을 사용)
*iterative minimization 기법 종류 : gradient descent 방법, 가우스-뉴턴법, Levenberg-Marquardt 방법 등
[Levenberg-Marquardt 알고리즘]
- 관측값을 (xi, yi), i=1,...,n,
- 모델 파라미터를 p = ( p1, p2, ..., pm) ,
- 모델을 y = f(x, p),
- 오차(residual)를 ri(p) = yi - f(xi,p)라 하고
- 최소화시키고자 하는 목적함수를 E(p) = ∑ri(p)^2라 하면
- E(p)를 최소화시키는 해는 모델 파라미터 p에 대한 초기 추정값 p0=(p10,...,pm0)에서 시작하여 p를 다음 수식에 의해 반복적으로 갱신함으로써 얻어짐

- 식 (33), (34)에서 μ는 매 iteration마다 변하는 damping factor로서 μ를 어떻게 계산하느냐에 따라서 다양한 방식의 Levenbarg-Marquardt 알고리즘 구현이 가능
- 구체적인 방법은 조금씩 다르겠지만 그 기본적인 원리는 현재의 μ값을 가지고 p를 갱신했을 때 E(p)가 증가했다면 E(p)가 감소할 때까지 μ를 계속 증가시키고, E(p)가 감소하면 μ를 원래의 기본적으로 설정된 값(최소값)으로 낮추는 원리
'AI study' 카테고리의 다른 글
| 부스팅 앙상블 (Boosting Ensemble) 2-1: Gradient Boosting for Regression (0) | 2022.08.21 |
|---|---|
| Multi Objective Optimization with GA원리 (0) | 2022.08.17 |
| Object Detection (0) | 2022.08.14 |
| Contour features (0) | 2022.08.13 |
| ML이나 image processing에서 grayscale image를 사용해야 하는 이유 (0) | 2022.08.13 |