2022. 7. 20. 10:30ㆍ인공지능,딥러닝,머신러닝 기초
1. MLP(다중 선형 회귀 분석(Multiple Linear Regression)
- 복수개의 독립변수를 가지고 종속 변수를 예측하기 위한 선형회귀모델로 식(3)에서 x : 독립변수, β는 각 독립변수의 계수, ε은 잔차
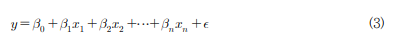
- 선형회귀분석에서 회귀계수(coefficient)의 추정량을 구하기 위해서는 식(4)로 표현되는 최소자승법(least squared method)을 사용한다

- 독립변수의 개수가 많아지게되면 변수들 사이의 높은 상관관계로 인해 다중공선성의 문제 발생가능성있으나
독립변수의 개수를 줄이는 것은 모델의 최적화에 대한 한계를 수반함
2. SVR(Support Vector Regression) : kernel based learning
- SVM은 binary classification을 하기 위한 방법, SVR은 함수를 추정하여 연속적인 수치변수를 예측하는 회귀방법
2-1. 함수추정의 목적
- 함수를 추정하고 싶을 때 목적 크게 2가지로 나뉨
a. Minimize an error measure(Loss function) : error 최소화
b. Function to be simple : 같은 성능이라면, 함수는 최대한 단순해야함(단순함의 조건은 아래와 같음)
- Fewest basis funcions
- Simplest basis functions
- Flatness is desirable
- Loss function과 Flatness를 반영하도록 목적함수 만듦
- SVR에도 여러 종류가 있음 그중에서도 먼저 ε-SVR에 대해서 알아보자
- 현실 Data들은 어쩔수 없이 발생하는 noise가 존재, 아래식에서 noise는 ε
y=f(x)+ε
- ε-SVR에서 핵심 아이디어는 ε보다 작은 noise에 대해서는 Loss를 주지 말자는 것

- 위 그림에서 색칠해진 영역을 Epsilon-tube라고하는데 이영역안에 있는 객체들에게는 Loss를 부여하지 않음
- 이를 위한 Loss function은 오른쪽에 표현됨 : 이 Loss function은 hinge를 닮았다고 해서, Hinge Loss라고 불림
- >차이가 ε 보다 작은 경우 loss는 0이고, ε 보다 큰 경우 선형적으로 ξ만큼의 loss를 받음
- >Squared loss를 사용하는 경우와 비교했을 때 noise에 더 robust하고, 선형적으로 loss가 계산됨으로 out liar에 덜 민감

2-2. Hinge loss를 사용한 SVR을 Formulate
- Estimating a linear regression : 목표는 미지수 w와 b를 알아내는 것

- Optimization problem with precision ε

- SVM에서 (1/2)||w||^2 항은 Margin을 최대화 하는 역할
-> 하지만 SVR에서는 Flatness를 최대화 하는 역할
- SVR에서 Loss를 최소화 하는 부분 : C∑ni=1(ξi+ξ∗i) term -> C는 Loss와 Flatness간의 trade-off를 조정하는 Hyperparameter임
- 제약식을 살펴보면 (1)과 (2) 2개가 있음
- 각 제약식은 한번에 적용되는 것이 아니라 Estimate 된 함수의 아래에 있는 객체에는 (1)번이, 함수의 위에 있는 객체에는 (2)번이 적용됨
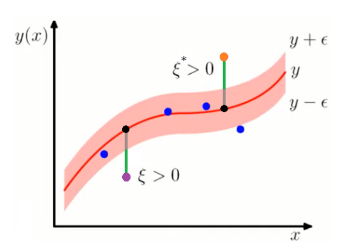
- 먼저 함수 아래쪽에 위치한 보라색 point : 해당Xi값에 대하여 함수가 추정하는 값은 wTx+b 으로, 그림에서 검은 점에 해당함(1)- 검은 점에게 부여되는 Loss ξ는 (wTx+b)−yi−ϵ- 초록샌 선이 Loss ξ를 나타냄 -> 이에대한 제약식이 (1)임(2)
- 함수의 위쪽에 위치한 주황색 point를 살펴보면, 위에서 본 것과 동일하게 xi 값에 대하여 함수는 wTx+b 를 추정할 것
- 이때 Loss ξ∗는 yi−(wTx+b)−ϵ -> 이에대한 제약식이 (2)임
라그랑주 승수법 (Lagrange Multiplier Method)
라그랑주 승수법 (Lagrange multiplier method)은 프랑스의 수학자 조세프루이 라그랑주 (Joseph-Louis Lagrange)가 제약 조건이 있는 최적화 문제를 풀기 위해 고안한 방법이다. 라그랑주 승수법은 어떠한
untitledtblog.tistory.com
- Primal Lagrangian
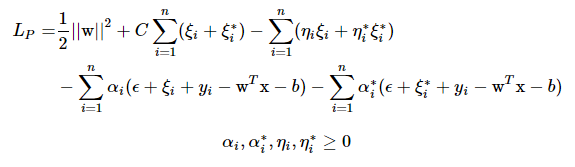
- KKT Condition에 따라 미지수 b,w,ξi,ξ∗i로 미분한 값은 0 이어야 함
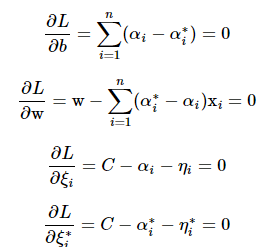
https://yupsung.blogspot.com/2021/01/support-vector-regression-svr.html
- Dual Lagrangian problem
- SVR(Support Vector Regression)은 학습 데이터의 분류 예측 에 사용되는 SVM을 ε-무감도 손실함수를 도입하여, 임의의 실수 값을 예측하도록 일반화한 방법

- 위 그림에서 각각 클래스의 최외각 벡터(support vector)를 지나는 직선을 각각

로 표현할 수 있고, 각 클래스 데이터는 이 직선들 위, 또는 아래에 존재하기 때문에 식 (5)의 조건을 만족해야함

- 이때 클래스를 나누는 두 직선 사이의 거리는

가 되고, 클래스간 거리를 최대로 하는 것이 SVM 목적이기 때문에 |w|를 최소화시켜야함
- 이를 위해 식(6)과 같은 라그랑지 상수를 이용함

- 식 (6)에서 α는 라그랑지 상수이고 yi는 입력 데이터 클래스 에 대한 값임
- yi에 대한 식은 (7)과 같음

- 아래 그림2는 SVR개념도임

- SVM과 유사하게 실제 값과 예측값의 차이를 최대한 ε 이내로 유지시키는 것이 목적
- ε 는 오차 허용률(또는 epsilon width of tube)이라고 하며, 사용자에 의해 선택
- 예측 성능을 나타내는 오차는 f(x) (+/-) ε 경계선과의 거리로 게산
- SVR의 비선형 확장은 SVM과 마찬가지로 선형적으로 분리가 가능하지 않은 원래의 특징 공간을 더 높은 차원의 새로운 공간으로 변환하여 수행함
- 즉, 커널 함수를 사용하여 입력 공간의 저차원 비선형 회귀문제를 사상을 통해 고차원 선형 회귀문제로 변환
[참고: " MLR 및 SVR 기반 선형과 비선형회귀분석의 비교 - 풍속 예측 보정" (2016) (김 준 봉* ․외) ]
'인공지능,딥러닝,머신러닝 기초' 카테고리의 다른 글
| [DL] DNN(Deep Neural Networks) 성능 개선 (0) | 2022.08.02 |
|---|---|
| Optimization : Lagrange Dual Problem & Strong duality and Karush-Kuhn-Tucker Conditions (0) | 2022.07.20 |
| ANN (0) | 2022.07.18 |
| [Do it! 딥러닝 입문] 4장 1절~2절 로지스틱 회귀와 시그모이드 함수 (0) | 2022.07.17 |
| 머신러닝 스태킹 앙상블(stacking ensemble)이란? _ CV(Kfold) (0) | 2022.07.16 |